Minimum Fuel Cost to Report to the Capital

In this problem, we are given a tree structure of a city plan. By that, it means that we have a graph of $n$ nodes that consists of exactly $n-1$ edges. The graph is also connected, i.e., it is possible to travel from one city to any other one. The setting is that the capital city is marked at node 0, and every other city has one representative that needs to come to the capital. They can travel together in a car, which has a limited number of seats. The problem asks us to find the minimum number of fuels used, considering that moving from one to another city takes exactly 1 liter of fuel.

Intuition

This problem can seem daunting at first, but take a look at the below example to understand what we are trying to do.

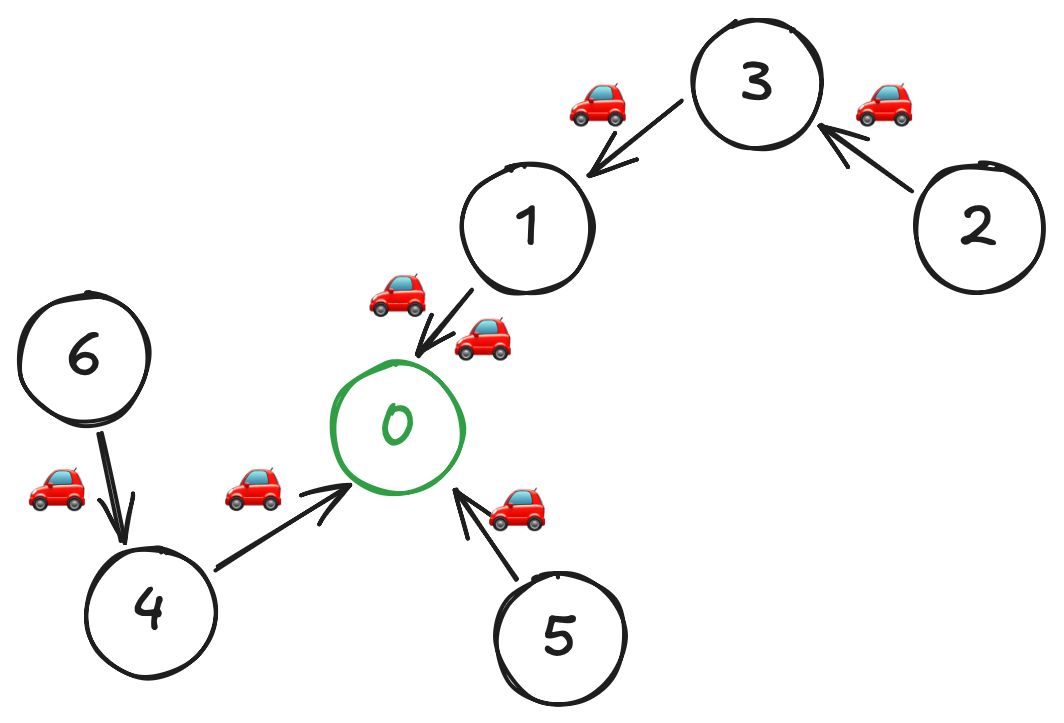
Walkthrough

In this example, we only allow two passengers per car; the fuel required is exactly 7 liters. Observe that, since each edge requires 1 liter of fuel, we can think of the problem as counting how many cars it takes to pass that edge. The optimal solution requires us to be greedy and try to maximize the number of passengers in each car. Doing this will minimize the number of cars that need to pass through each edge, which in turn minimizes the fuel cost.

So now, we kind of have a rough idea that in each travel on the edge, if we know the number of cars required, we will be able to accumulate answers upon that. Now, how do we determine the number of cars required?

In the above example, traveling from city 2 to 3 requires 1 car since there is 1 passenger traveling from 2 to 3. When traveling from 3 to 1, we have 2 passengers, and we can fit them in 1 car. However, after we pick up the passenger from 1, we now have 3 passengers, and since we can only fit 2 in a car, we will need 2 cars to travel from 1 to 0.

Mathematical Formulation

So, think of it this way: we know that the number of passengers on each node is always 1. If we can count the total passengers from all previous nodes, the total passengers will be 1 (the node itself) + the sum of passengers from all its children nodes.

Once we have that, we can easily calculate the number of cars required to travel from that node to its parent by calculating $\displaystyle\lceil\frac{\text{total passengers}}{\text{seats}}\rceil.$

Implementation

Depth-First Search (DFS)

First, let's consider a helper DFS function that will return the total number of passengers from that node to all its children nodes.

#include <vector>
using namespace std;

int dfs(int node, int parent, int seats, long long& fuels, vector<vector<int>>& adj) {
    int passengers = 1; 
    for (int& nbr : adj[node]) { 
        if (nbr == parent) continue; // Avoid going back to parent
        int sub = dfs(nbr, node, seats, fuels, adj);
        passengers += sub;
        fuels += (sub + seats - 1) / seats; // Ceiling
    }
    return passengers;
};

Here, we denote adj as the adjacency list of the graph. Since this is recursion, the computation is done from bottom-up; it means that the deepest node is processed first, then we accumulate the total passengers upon. The node we will specify when calling this initially is 0, the capital city. We can set the parent of that node to be -1, since it doesn't have a parent.

tip

In other languages, you may use the ceiling function directly, but in C++, we can use the trick of adding seats - 1 before.

Final Code

Below is the final code that uses the above helper function to compute the final answer.

long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
    int n = roads.size() + 1;
    vector<vector<int>> adj(n);
    for (auto& r : roads) {
        adj[r[0]].push_back(r[1]);
        adj[r[1]].push_back(r[0]);
    }
    
    long long fuels = 0;
    dfs(0, -1, seats, fuels, adj);
    return fuels;
}

Notice how we first build an adjacency list from the given edges. This is a standard practice to save space and allow fast access to the neighbors of each node.

We also pass a reference to the fuels variable to the DFS function, so that we can accumulate the answer as we go through each node. We may need an extra function if we are not allowed to use a reference. The time complexity of this solution is $O(n)$, since we only visit each node once.